Inteligencia Artificial con Lógica Fuzzy y su aplicación en el mundo real

En este tutorial aprenderemos cómo la Lógica Fuzzy puede ayudarnos a expresar incertidumbres de manera más consistente, a través de conjuntos difusos, "en lugar de simplemente pertenecer o no pertenecer y así lidiar con la ambigüedad de la información y la incertidumbre del mundo real".

Varias herramientas tecnológicas actuales nos han permitido brindar una mejor orientación en diversas áreas de mejora del servicio. Entre las técnicas de Inteligencia Artificial (IA) más utilizadas en el desarrollo de sistemas inteligentes se encuentran las redes neuronales artificiales (ANN), las redes neuronales convolucionales (CNN), las máquinas de vectores de soporte (SVM), la lógica difusa y los árboles de decisión (DA).

En mi artículo anterior sobre el uso de la Inteligencia Artificial para la clasificación con la técnica del Árbol de Decisión, explico cómo los ADs pueden generar reglas del tipo SI...ENTONCES, que también podemos usar en conjunto con la Lógica Difusa, convirtiéndolo en un trabajo más integral y robusto en cuanto a técnicas de IA para predecir factores que ayuden a las empresas en la toma de decisiones.

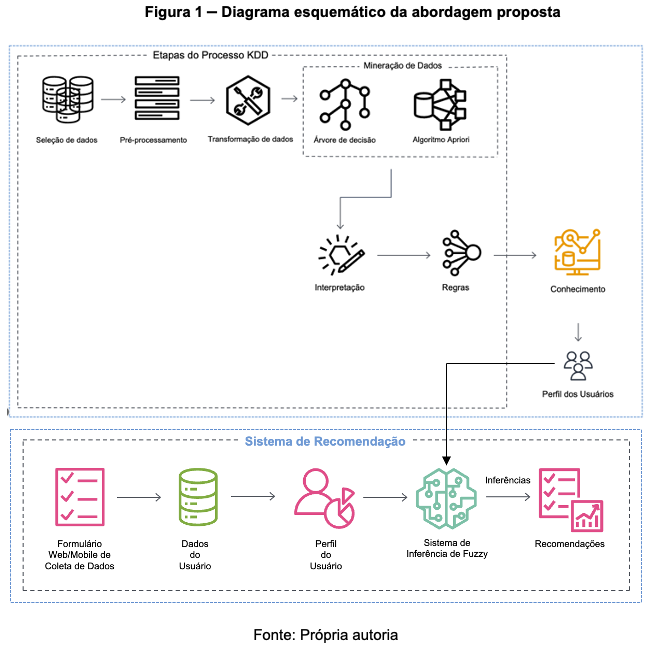
Los AD forman parte del Data Mining junto con otras técnicas, como el uso del algoritmo Apriori. En la figura 1 podemos ver un conjunto de técnicas de IA que pueden usarse para el desarrollo de una técnica de inteligencia artificial.

Varias herramientas tecnológicas actuales nos han permitido brindar una mejor orientación en diversas áreas de mejora del servicio. Entre las técnicas de IA más utilizadas en el desarrollo de sistemas inteligentes destacan las redes neuronales artificiales (ANN), las redes neuronales convolucionales (CNN), la Máquina de Vectores de Soporte (SVM), la Lógica Fuzzy y los Árboles de Decisión (AD).

En este artículo quiero presentar cómo la Lógica Difusa, o Lógica Fuzzy, puede ayudarnos a desarrollar sistemas matemáticamente no tradicionales. La palabra Fuzzy en inglés puede tener varios significados, que cambian según el contexto. "Nebulosa" y "difusa" son algunas de las traducciones más comunes (BEZERRA, 2010), pero el significado fundamental de este adjetivo siempre está relacionado con algo vago, indistinto e incierto.

La lógica difusa o Lógica Fuzzy es una forma de lógica multivalorada (o multifunción) en la que los valores de verdad de las variables pueden ser cualquier número real entre 0 y 1, a diferencia de lo que ocurre en la lógica booleana, según la cual los valores lógicos ​​puede ser simplemente 0 o 1. Es decir, es un estudio que utiliza la lógica matemática para presumir soluciones y resolución de problemas, incluso con la imprecisión de datos e información, pero que permite obtener conclusiones precisas.

Se considera una forma de lógica que trata con modelos de razonamiento imprecisos o aproximados (ZADEH, 1973). Esta lógica permite trabajar con problemas de decisión que no se representan fácilmente en modelos matemáticos convencionales. Un control Fuzzy busca “imitar” a un agente humano a través de una descripción descriptiva y experimental de un proceso específico (ZADEH, 1973).

Dentro del campo de la Inteligencia Artificial, la Lógica Fuzzy es considerada un mecanismo fundamental para representar adecuadamente el conocimiento y el razonamiento, debido a su capacidad para trabajar con incertidumbres, razonamientos aproximados, términos vagos y ambiguos, que son formas en que las personas expresan sus pensamientos.

Por lo tanto, los sistemas Fuzzy tienen la capacidad de "razonar" teniendo en cuenta perspectivas relacionadas con la incertidumbre y los procesos prácticos, haciéndolos más similares al comportamiento "humano" (BEZERRA, 2010), como se muestra en la Figura 2.

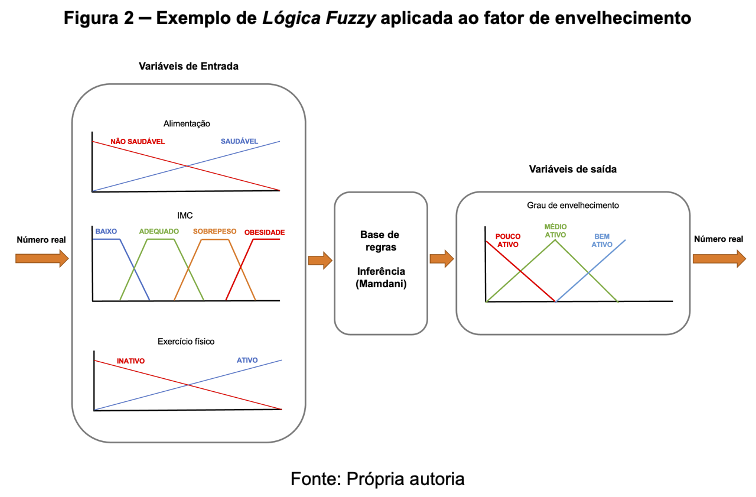
Esta técnica del campo de la inteligencia computacional permite la representación de situaciones del mundo real. Además, se centra en cómo codificar software que represente algoritmos más cercanos a la forma en que funciona el razonamiento humano.

Los principios de esta lógica tuvieron su origen en los estudios del Prof. Lotfi A. Zadeh en 1965 en la Universidad de California, Berkeley. Podemos decir que la inteligencia humana tiene la cualidad de "nebulosidad", pues tiene la posibilidad de resumir los hechos observados y, aunque tiene una amplia capacidad para adquirir información, puede seleccionar los más relevantes. En la teoría de conjuntos clásica, podemos decir que un elemento pertenece o no pertenece a un conjunto, es decir, siempre tenemos la condición de falso o verdadero (lógica bivalente).

El profesor Zadeh, como se menciona en Dubois y Gomide, ha propuesto una caracterización más amplia al sugerir que algunos elementos son más miembros de un conjunto que otros. El grado de membresía o grado de certeza puede entonces asumir cualquier valor entre 0 y 1, donde el valor 0 indica exclusión completa y el valor 1 representa membresía completa. Esta generalización aumenta el poder de expresión de la característica función (lógica multivalente) (ZADEH, 1973).

La siguiente es una lista no exhaustiva de dominios de aplicaciones de Fuzzy Logic:

• Sistemas especialistas;
• Sistemas multiagentes;
• Reconocimiento de patrones;
• Robótica;
• Sistemas de control inteligentes;
• Sistemas de apoyo a tomas de decisión;
• Algoritmos genéticos;
• Data Mining.

McNeil y Thro (1994) relacionan algunas características de los sistemas en los que la aplicación de la Lógica Fuzzy resulta beneficiosa:

• Sistemas complejos difíciles o imposibles de modelar;
• Sistemas controlados por especialistas (humanos);
• Sistemas con entradas y salidas complejas y continuas;
• Sistemas utilizados en la observación humana como entradas o como base para reglas;

Sistemas que son naturalmente “vagos”, como los que involucran a las ciencias sociales y del comportamiento, cuya descripción es extremadamente compleja.

Como lo Fuzzy funciona en relación con las funciones matemáticas clásicas

En el contexto matemático, la idea de relación se expresa a través de la teoría de conjuntos. Por lo tanto, intuitivamente, podemos clasificar una relación como difusa cuando se adopta la teoría de conjuntos difusos, o como clásica cuando se utiliza la teoría de conjuntos clásica para definir la relación bajo análisis.

La elección entre estos dos modelos depende del fenómeno que se estudie. Sin embargo, optar por la teoría de conjuntos difusos es generalmente más completo, ya que abarca la teoría de conjuntos clásica.

Una relación clásica sigue la función característica de la lógica clásica. Por ejemplo, considere una relación de amistad entre dos personas llamadas "amigos". En este caso, el enfoque clásico considera que en las relaciones humanas, o alguien es amigo del otro o no lo es, lo que supone una simplificación de la realidad.

En la relación de amistad difusa se tiene en cuenta el grado de amistad entre las personas, permitiendo que dos o más individuos se relacionen con diferentes grados de amistad, que van desde 1,0 (que indica amistad completa) hasta 0,0 (que indica ausencia de amistad).

Formalmente, una relación fuzzy R entre dos variables, x ∈ a X y y ∈ a Y, es definida por una función que mapea el par ordenado (x, y) en el espacio X x Y para su grado en la relación, es decir, R: X x Y -> [0,1]. Esa definición puede ser extendida fácilmente para relaciones de dimensiones superiores.

Ahora que entendemos las definiciones de la Lógica Fuzzy, comencemos a declarar las variables de entrada y de salida de nuestro Sistema de Inferencia Fuzzy. Para ello, utilizaremos como modelo un sistema que calcula los niveles de satisfacción de los servicios en un restaurante. Las variables de entrada serán la calificación del servicio y la calificación de la comida. Y la variable de salida será cuánta propina o cargo por servicio se estaría dispuesto a pagar.

Antes de comenzar a definir las variables de entrada, debemos recordar, como en el ejemplo de amigos anterior, que estamos hablando de un enfoque no clásico, donde el grado de amistad se definirá más allá de si es un amigo o no, es decir, valores entre 1,0 y 0,0. Para ello, hacemos uso de variables lingüísticas que tienen valores que no son números. Son nombres de conjuntos difusos que se pueden representar mediante funciones de membresía, mostradas en la Figura 2 para factores de envejecimiento en relación al IMC (bajo, adecuado, sobrepeso, obesidad).

Usando el "problema de la propina" para ejemplificar nuestra lógica difusa

El "problema de la propina" se utiliza comúnmente para ilustrar el poder de los principios de la lógica difusa para generar comportamientos complejos a partir de un conjunto compacto e intuitivo de reglas especializadas.

Crearemos un sistema de control difuso que modele cómo elegirías dar propina en un restaurante. Cuando das propina, consideras el servicio y la calidad de la comida, calificándolos entre 0 y 10. Usas esto para dejar una propina entre 0 y 25%, dependiendo del país y la costumbre.

Formularíamos el problema como:

Iniciando la declaración de las variables

Variables de entrada (inputs) - antecedentes

Servicio

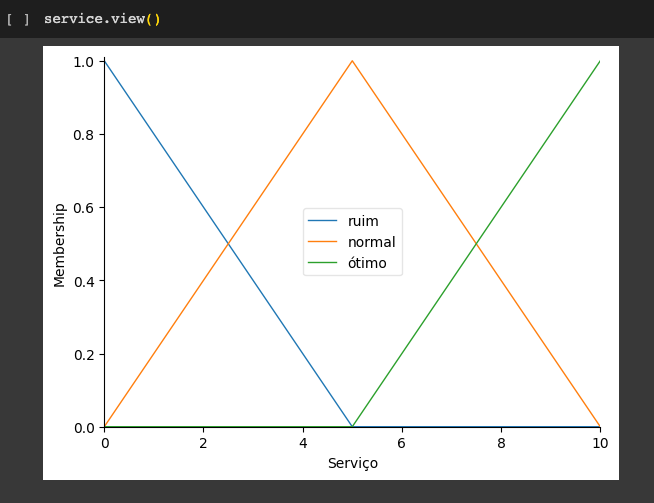
• Universo (es decir, franja de valor nítido): ¿Cuán bueno fue el servicio del equipo de meseros, en una escala de 0 a 10?: Malo, normal, excelente.
• Conjunto difuso/fuzzy (franja de valores difusos): malo, normal, excelente.

Comida

• ¿Cómo calificas la comida (0-10)?: mala, normal, excelente.
• Conjunto difuso/fuzzy: mala, normal, excelente.

Variables de salida (outputs) - consecuentes

Tasa de Servicio/Propina

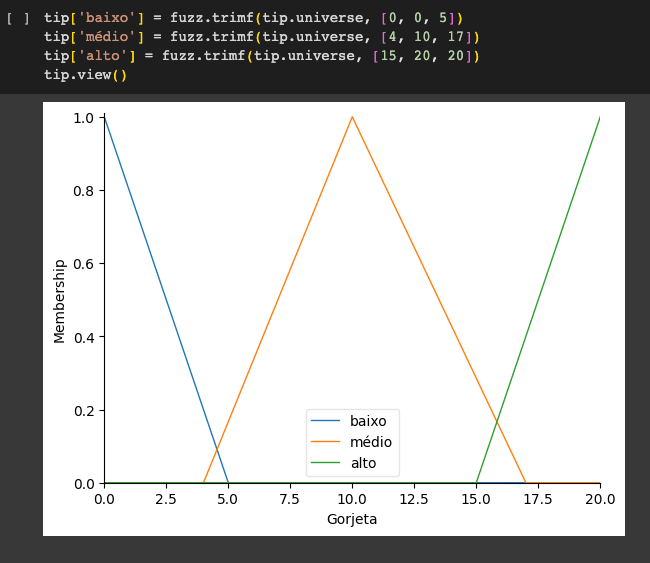
• Universo: Cuánto debemos dar de propina, en una escala de 0% a 20%.
• Conjunto difuso/fuzzy: bajo, promedio, alto.

Reglas

• SI la calidad de la comida fuera mala O la calidad del servicio fue mala, ENTONCES propina será baja.
• SI la calidad del servicio fuera normal, ENTONCES la propina será promedio.
• SI la calidad del servicio fuera excelente Y la calidad de la comida fuera excelente, ENTONCES la propina será alta.

Uso

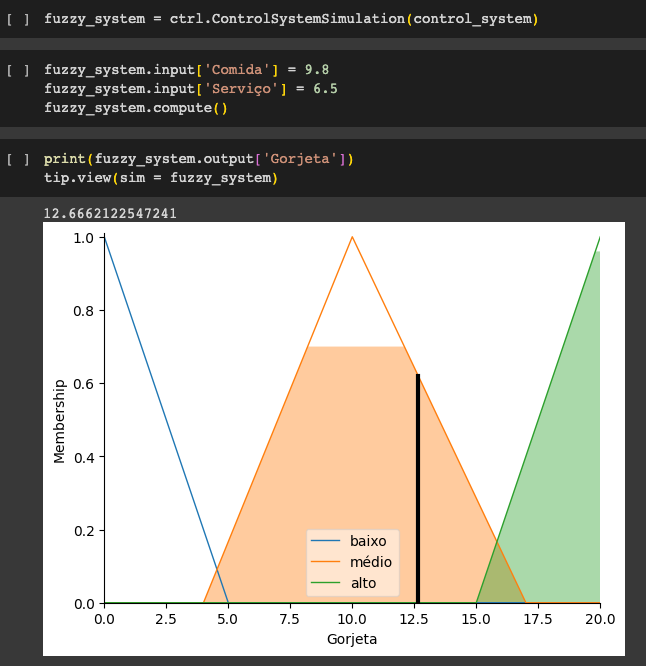
Si le digo a este controlador que he evaluado:

• El servicio como 9.8, y
• La calidad como 6.5,
• Recomendaría dejar:
• Una propina de 12.6 %.

Toda la documentación de Scikit Fuzzy la hallarás aquí.

Instalación de la biblioteca scikit-fuzzy

Importar la biblioteca scikit-fuzzy

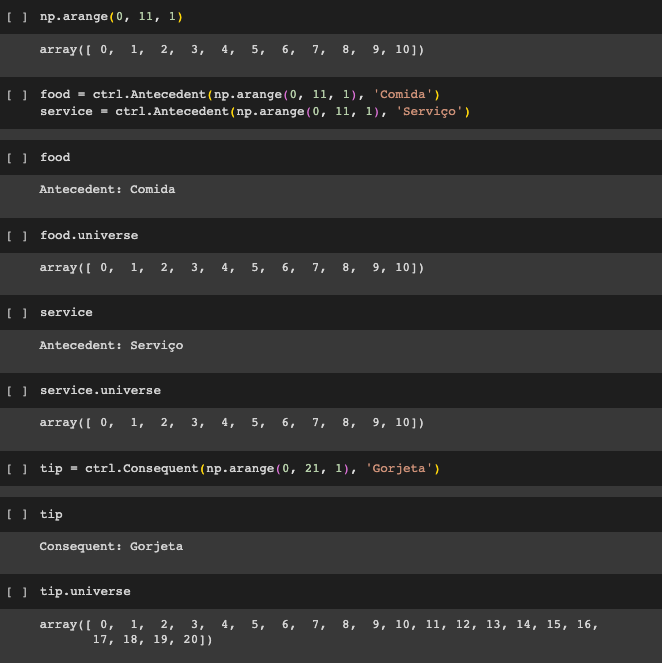
Declaración del universo/range de actuación de las variables antecedentes y consecuentes

Definición de las funciones de pertenencia

Imprimir las funciones de pertenencia

Imprimir las funciones de pertenencia en la variable excelente (ótimo)

Imprimir las funciones de pertenencia en la variable mala (ruim)

Imprimir las funciones de pertenencia en la variable normal

Imprimir las funciones de pertenencia para las variables de servicio

Imprimir el universo de pertenencia de los valores de propina

Imprimir las funciones de pertenencia de la variable de propina

Reglas difusas/fuzzy

Ahora, para que estos triángulos sean útiles, definimos la relación difusa entre las variables de entrada y salida. Para los propósitos de nuestro ejemplo, considera tres reglas simples:

• SI la calidad de la comida fuera mala (ruim) O la calidad del servicio fuera mala (ruim), ENTONCES la propina será baja.
• SI la calidad del servicio fuera normal, ENTONCES la propina será promedio.
• SI la calidad del servicio fuera excelente (ótimo) Y la calidad de la comida fuera excelente (ótima), ENTONCES la propina será alta.

La mayoría de las personas coincidiría con esas reglas, pero éstas son confusas. Mapear reglas imprecisas en un apartado definido y aplicable es un reto. Este es el tipo de tarea donde se destaca la Lógica Fuzzy.

Imprimir las reglas del Sistema de Control Fuzzy, conectando antecedente(s) y consecuente(s)

Creación y simulación del Sistema de Control

Ahora que tenemos nuestras reglas definidas, simplemente podemos crear un sistema de control mediante:

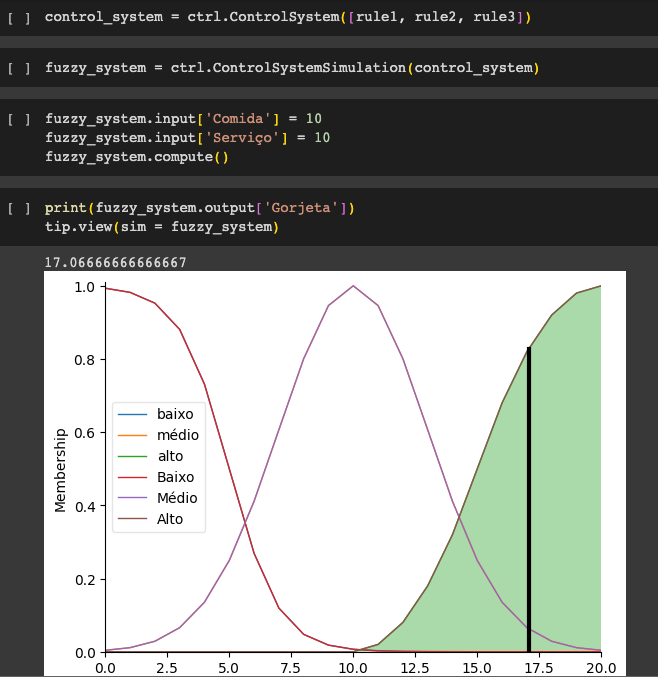
Para simular este sistema de control, creemos un ControlSystemSimulation. Piensa en este objeto como si representara nuestro controlador aplicado a un conjunto específico de circunstancias. Dar propina, esto podría ser como darle propina a un camarero en un bar.

Cuando intentamos aplicar nuestro "Control de Propinas" a otro establecimiento, como una cafetería, crearíamos otro ControlSystemSimulation porque las entradas serían diferentes.

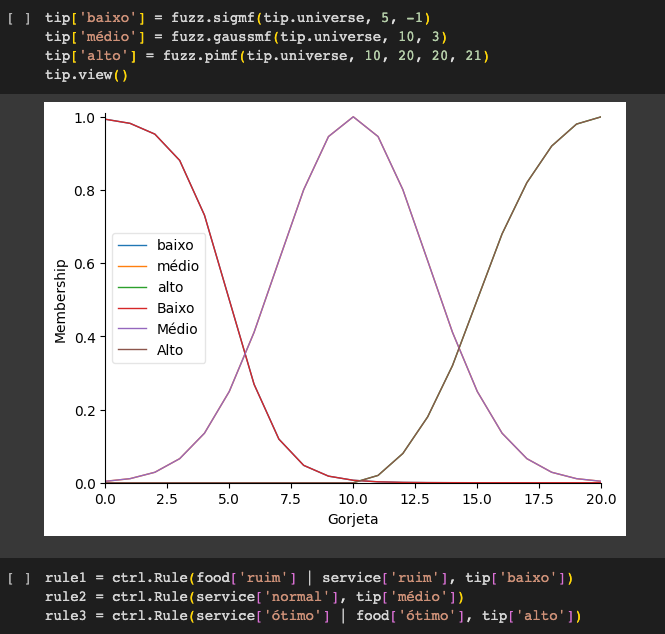
Imprimir funciones de pertenencia usando la distribuición Gaussiana

Conclusión

El poder de los sistemas difusos es permitir un comportamiento intuitivo y complicado basado en un sistema disperso de reglas con una sobrecarga mínima.

Ten en cuenta que nuestros universos de funciones de membresía eran aproximados, definidos solo en números enteros, pero fuzz.interp_membership permitió que la resolución efectiva aumentara según la demanda. Este sistema puede responder a cambios arbitrariamente pequeños en las entradas y la carga de procesamiento es mínima.

¡Hasta la próxima!