Cómo funciona una inteligencia artificial - Redes neuronales

La Inteligencia Artificial es una de las tecnologías de mayor crecimiento en la actualidad y está presente en varias aplicaciones de nuestro día a día, como asistentes virtuales, coches autónomos y sistemas de recomendación. Una de las áreas más importantes de la Inteligencia Artificial es el Aprendizaje Automático o Machine Learning, que permite que los sistemas aprendan de los datos sin ser programados explícitamente.

En este artículo hablaremos sobre una de las técnicas de Machine Learning más poderosas y versátiles que son las redes neuronales, incluido aprender a implementar una desde cero en Python.

¿Qué son las redes neuronales?

Las redes neuronales son algoritmos modelados sobre el funcionamiento de las neuronas biológicas. Cada una de las neuronas, también llamada perceptrón, puede estar interconectada entre sí en diferentes capas.

Básicamente, el perceptrón es una unidad de procesamiento de información simple. Tiene dos funciones: la función de suma, que sumará los valores de todas las entradas multiplicadas por sus respectivos pesos, y la función de activación, que tomará el valor de la función de suma para transformarlo en una salida, la cual variará según la activación elegida. Por ejemplo, la función step devuelve 0 (cero) si el valor está por debajo de cierto umbral, y 1 si está por encima.

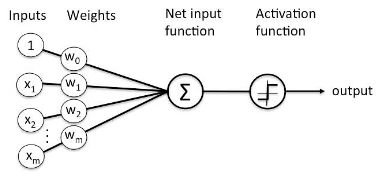
Cuando se conectan en secuencia, en diferentes capas, los perceptrones permiten crear funciones más complejas que pueden ajustarse mejor a los datos y producir patrones interesantes. Lo que determinará la eficiencia de la red son los pesos, los cuales pueden entenderse como la relevancia que tiene cada parámetro de entrada para obtener el patrón de comportamiento esperado. Es decir, los pesos son el “conocimiento” de la red.

Cómo aprenden las redes - Algoritmos de optimización

La parte más interesante es cómo hacemos para encontrar el valor de cada peso. El enfoque más simple sería probar con fuerza bruta todas las combinaciones posibles de pesos, algo que podría funcionar en problemas simples, pero a medida que aumenta la complejidad del problema, se vuelve inviable probar todas las combinaciones posibles: con cada nueva prueba que se hace, la red está comenzando desde cero.

Aquí es donde entran los algoritmos de optimización, que hacen que la red se adapte de acuerdo a los datos de prueba, por ejemplo, digamos que generamos una red con pesos aleatorios y el resultado devuelto fue 0.8, mientras que el resultado esperado fue de 1, entonces generamos otra red y volvemos a probar, esta vez el resultado obtenido fue 0.9, que aún no es el resultado que queremos, pero ya está más cerca de 0.8.

Existen varios tipos de algoritmos que buscarán el mejor valor de los pesos, pero lo importante es saber que aún no hay consenso sobre cuál es el mejor, después de todo esto sigue siendo un área de estudio por parte de científicos y la combinación de diferentes técnicas puede dar como resultado un algoritmo que sea más rápido y utilice menos recursos, por lo que es necesario ver el trabajo que ya se ha hecho, lo que se está haciendo ahora e intentar adaptarse a cada problema.

Uno de estos algoritmos se llama descenso de gradiente, el cual se utiliza para optimizar funciones matemáticas, en resumen, el objetivo es encontrar el mínimo (o máximo) de una función. El algoritmo funciona de forma iterativa, es decir, en cada iteración realiza una pequeña actualización en los parámetros de la función que se está optimizando. Esta actualización se realiza en la dirección del gradiente, que es una medida de la pendiente o pendiente de la curva de la función en un punto dado. En este algoritmo, se utiliza la derivada para saber si el valor es creciente o decreciente en relación al anterior y poder actualizar los pesos junto con otro algoritmo llamado backpropagation.

Otro posible enfoque, además de las matemáticas puras, es el uso de algoritmos genéticos, que buscan simular el proceso evolutivo de los seres vivos. Primero, se crea una población de diferentes redes neuronales con pesos definidos aleatoriamente para cada conexión, luego se prueban los individuos y se le asigna a cada uno de ellos una puntuación, también llamada fitness, que se utilizará para determinar la probabilidad de que un individuo sea seleccionado para hacer el crossover y crear los siguientes individuos en la población. Cuanto mayor sea el fitness, mayor la probabilidad.

Programando una red neuronal desde cero

A continuación, crearemos una red neuronal para ejemplificar, utilizando un problema de clasificación binaria simple. Primero, definamos el problema: tendremos un conjunto de datos con dos variables de entrada (x1 y x2) y una variable de salida (y), que puede ser 0 o 1. Nuestro objetivo es entrenar una red que sea capaz de clasificar las entradas correctamente.

Para simplificar el problema, generemos un conjunto de datos con 500 ejemplos. Cada ejemplo tendrá dos variables de entrada generadas aleatoriamente a partir de una distribución uniforme entre 0 y 1, si la suma de las dos variables es mayor que 1, la variable de salida se establecerá en 1. De lo contrario, debería devolver 0.

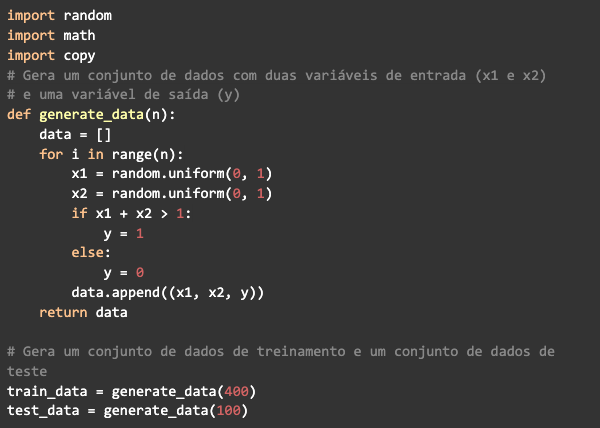
También crearemos una función de activación para las neuronas. En este ejemplo, usaremos el sigmoide:

A continuación, crearemos la clase de red neuronal y comenzaremos los pesos al azar. Esta red tendrá una topología fija, con dos neuronas de entrada conectadas a tres neuronas ocultas y estas tres neuronas ocultas estarán conectadas a la neurona de salida.

En la inicialización de la red, también es opcional pasar una lista de pesos, esto será importante para generar la nueva población después del cruce. Hay una condición para definir los pesos, si la lista está vacía se generarán aleatoriamente, en caso contrario se definirán según su orden en la lista. Otra cosa que se definirá es el fitness, que se irá modificando a medida que se pruebe la red para saber qué tan cerca está del modelo ideal con el 100% de precisión que estamos buscando.

Después de la inicialización, creemos tres métodos para la clase de red neuronal, uno para devolver todos los pesos de la red en una sola lista, uno para incrementar la aptitud de la red y otro para obtener el fitness:

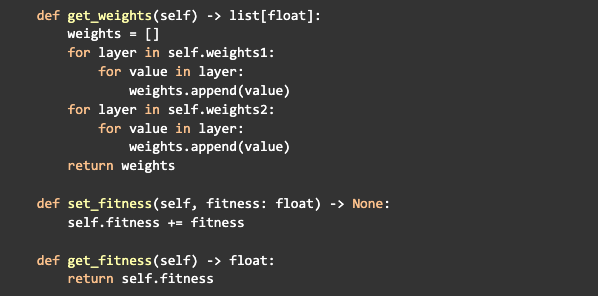
Lo siguiente que debe hacer es crear un método que propague la información a través de la red:

Las conexiones están dispuestas de modo que cada una de las entradas en las neuronas de entrada pase por una neurona en la capa oculta sola y la neurona del medio en la capa oculta tendrá conexiones con las dos neuronas de entrada. De esta forma, es posible analizar la relevancia de cada entrada individualmente y en conjunto en el resultado final.

Aún dentro de la clase de redes neuronales, crearemos otro método para generar mutaciones en los pesos, lo que será importante para agregar más varianza a los individuos después del cruce. Cada peso en la red tendrá un 80% de posibilidades de ser mutado y esta mutación tendrá un 90% de posibilidades de variar un 20% del valor actual y un 10% de posibilidades de recibir un nuevo valor aleatorio, luego definirá el nuevos valores de los pesos para la red:

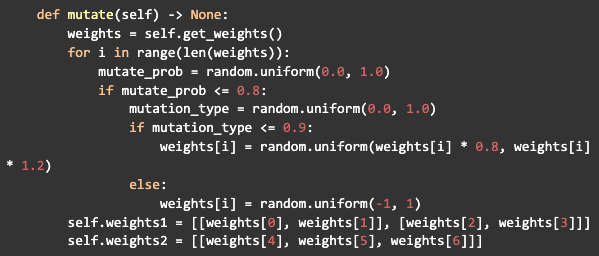
Con la red lista, se necesitará una función para calcular el fitness. Recibirá como parámetro la respuesta esperada y la respuesta obtenida, luego se calculará el error, que es la diferencia absoluta entre la respuesta correcta y la obtenida, luego se devolverá 1 menos el error, de esa forma, cuando el error es 0, se devolverá 1, cuando sea mayor que cero, la puntuación será menor que 1:

Finalmente, necesitamos una función de crossover para generar los nuevos individuos de la población y una función para seleccionar los individuos:

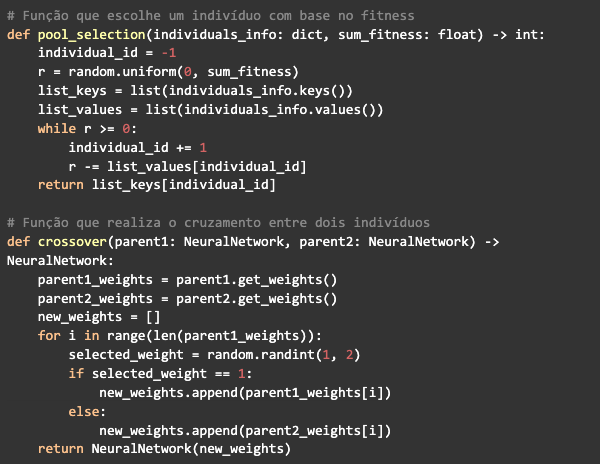
La selección se realiza mediante un algoritmo conocido como pool selection, recibirá un diccionario que contiene los ids referentes a la posición de los individuos en el array poblacional y su respectivo fitness, así como la suma del fitness de todos los individuos. Generará un número aleatorio entre 0 y la suma del fitness y comenzará a restar el valor del fitness de cada individuo de ese número generado, cuando es menor o igual a cero, devuelve la identificación del individuo que se detuvo.

Por lo tanto, todos los individuos tienen la posibilidad de ser elegidos para el crossover, pero su posibilidad de ser elegidos será proporcional al tamaño del fitness del individuo.

La función de crossover solo tomará los pesos de cada uno de los familiares seleccionados y compondrá los pesos del nuevo individuo, eligiendo aleatoriamente uno de los dos familiares, por lo que al final devolverá el individuo generado.

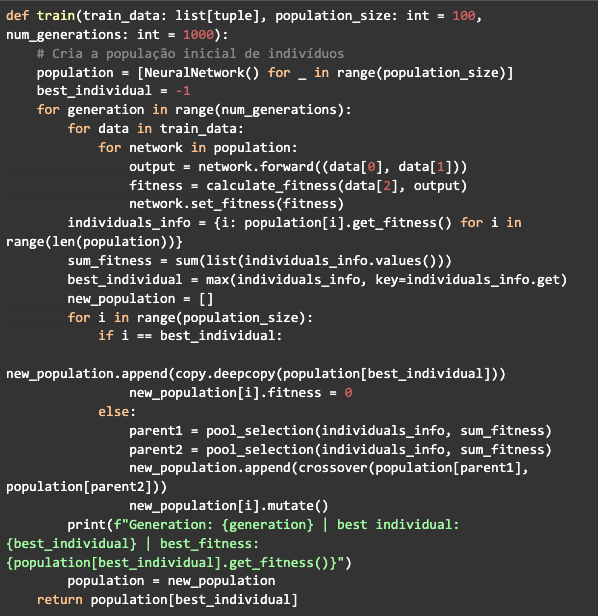
Ahora todo lo que tiene que hacer es juntar la clase de red neuronal y las funciones que hemos creado hasta ahora en una nueva función para entrenar la red. Esta función recibirá los datos de entrenamiento, el tamaño de la población y el número de generaciones. Creará un array del tamaño definido para la población con objetos de la clase NeuralNetwork que serán los individuos. Habrá un loop referente a la generación y dentro de él habrá otros dos lop, el primero tomará cada valor de la lista de datos, pasará por cada individuo haciendo la propagación, calculando y definiendo el fitness.

A continuación, se generará el diccionario con los id y el fitness de cada individuo, luego de lo cual se calculará la suma del fitness y se definirá el mejor individuo. Luego el segundo ciclo generará una nueva población, seleccionando los individuos con la pool selection y haciendo el crossover, pero al mismo tiempo conservando el mejor individuo encontrado en la generación, para que no pase por el crossover y no sufra mutaciones. para no cambiar su precisión. Después de pasar por todas las generaciones, la función de entrenamiento devolverá la red del mejor individuo:

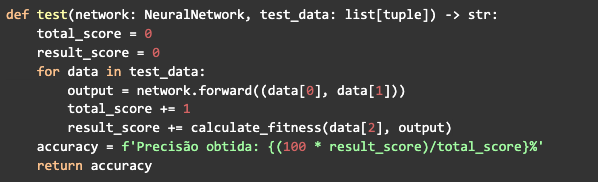
Finalmente, simplemente escribe una función para probar la red. Recibirás la red del mejor individuo y un conjunto de datos de prueba, se propagará y calculará el fitness para todos los datos. Dos variables medirán el rendimiento de la red, una sumará el valor máximo de fitness return para cada iteración, que es 1, y la otra sumará el valor obtenido. Así al final la función devolverá la precisión obtenida, que será una simple regla de tres con las variables que están midiendo el rendimiento. El total_score será 100% preciso y result_score es lo que se calculará:

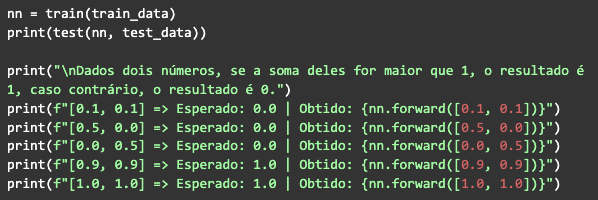
Una vez hecho esto, solo llama a la función de entrenamiento, luego a la de prueba. Con los datos que generamos al principio, ejecuta y observa el resultado:

Conclusión

La Inteligencia Artificial ha sido una de las áreas más prometedoras de la informática en los últimos años, y el Machine Learning ha despertado un papel clave en esta revolución. En particular, las redes neuronales son una de las técnicas de Machine Learning más poderosas, y el algoritmo genético es un enfoque interesante para optimizar el rendimiento de estas redes.

En este artículo, mostré cómo implementar una red neuronal desde cero en Python, usando el algoritmo genético para la optimización, sin usar bibliotecas externas. El código presentado puede ser una buena base para aquéllos quienes quieran entender cómo implementar redes neuronales y algoritmos genéticos.

Este ejemplo que usamos tiene una topología fija y está diseñado para resolver un solo problema, pero se puede adaptar para cambiar estáticamente la topología y resolver diferentes problemas. Sin embargo, existen soluciones más sofisticadas que también utilizan algoritmos genéticos y que, además de pesos, también evolucionan dinámicamente la topología de la red. Un ejemplo es NEAT y puedes consultar una forma de implementar este algoritmo en mi repositorio de GitHub.

¡Hasta pronto!